PROOF OF ICOSAHEDRAL CENTRE

 

 

Lemma 1

The 2 diagonals of a regular pentagon intersect each other in the ratio Ø : 1, where Ø is the golden mean defines as follows. Take a line AB and a point C on it. Then, if AB:AC = AC:CB we say that C divides AB in the golden  ratio, and that each of the above ratios is as Ø : 1. The value of Ø is approximately 1.618.

 

 

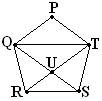
By symmetry PQ//TR and PT//QS Þ PTUQ  is a rhombus, in particular PT = QU ¾

                    Consider the similar (Isosceles) Ds, DRUS and DQUT

 

 

Then: 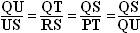 , the last equivalence by  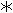above.

 

            i.e.  QU:US = QS : QU  and similarly  TU : UR = TR : TU     
which establish the lemma.

 

 

Lemma 2

                        A diagonal of a regular pentagon of side 1 has length Ø .

            Let the above ratios be equal to Ø, i.e. QT:RS = Ø  : 1.

If  RS = 1, then QT = Ø which establishes this lemma.

 

Proof proper: 

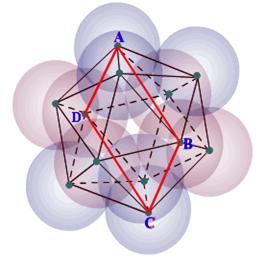
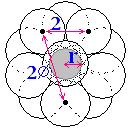
    Let the spheres of the icosahedral grouping have unit radius. (Distinguish between the icosahedron and the icosahedral-grouping)

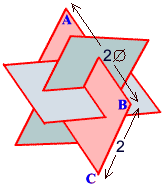
Within the icosahedron we can identify 3 planes which are mutually perpendicular, see diagram. Each plane is determined by 2 parallel edges of the icos. These 2 edges are 2 of the 4 edges of a rectangle. If the edge length of the icos. is 2 then this rectangle is 2 units wide and 2Ø units long (using Lemma 2).

 

              

 

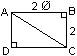Using Pythagoras: AC² = 2² + ( 2Ø )²  = 4 + 4Ø ²  = 4( 1+ Ø ² )

                         Þ  AC = 2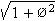

 

Now the diameter of this rectangle is the distance from an apex of the icos. to the opposite apex, i.e. it is the longest diameter of the icos. So, the radius of the circumscribing sphere of the icosahedron is 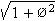_. In the icosahedral-grouping of spheres, this is the length of a line from the centre of the grouping to the centre of a ball (or the radius of a sphere through the centres of the 12 balls),

Þ Radius R of circumscribing sphere of the icosahedral-grouping (exosphere) is R = .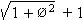 

 Similarly, the radius of the sphere that would fill the space inside the grouping (the endosphere, say) is

                                    r =

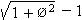
                                Þ Rr = 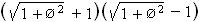 = Ø ²  ¾¾¾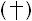  

                        Þ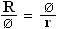   

But, (using the rectangle argument) 2 Ø is the diameter of a sphere passing through the points of contact of the 12 spheres, the “contact” sphere, i.e. Ø is its radius, say R_1.

           

             Þ R : R₁ = R₁ : r      

i.e. vol. of exo. : vol of contact  =  vol. of  contact : vol. of endo.

 

Using Lemma 1, Ø ²  =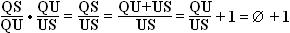

                     Þ Rr = 1 + Ø,  using 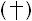 above.

Þ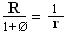     i.e.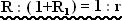

 

To calculate Ø , note that Ø ²  = Ø + 1, i.e. Ø ² -  Ø  - 1 = 0

              

           

 

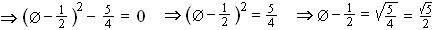
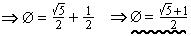
     So,

 

              

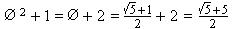
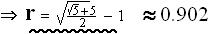
                                                                            Top view of the icos. grouping